Όταν ήμουν μαθητής ρώτησα τον καθηγητή των μαθηματικών πως υπολογίζεται το
ή "ακόμα χειρότερα" το
όπου e η βάση των νεπέριων λογαρίθμων, ο αριθμός e=2,718281828… που μεταξύ άλλων είναι και το όριο της ακολουθίας
όταν το ν τείνει στο άπειρο.
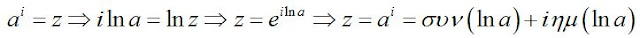
Όμως από που κι ως που ισχύει η εξίσωση;
Για έναν μαθητή λυκείου φαίνεται ακατανόητη ... αλλά γίνεται αμέσως κατανοητή διαμέσου των δυναμοσειρών, χρησιμοποιώντας τα παρακάτω αναπτύγματα
Τώρα είμαστε σε θέση να υπολογίσουμε και το i i
Το lni γράφεται
Οπότε:
και
Για κ=0 προκύπτει
Ο "δεύτερος τρόπος"
Στα μαθηματικά υπάρχει πάντα και ο "δεύτερος" πιο απλός τρόπος!
Έτσι, για να υπολογίσουμε το i i , εργαζόμαστε ως εξής - ξεκινώντας από την πιο όμορφη εξίσωση του κόσμου:
Υψώνουμε και τα δυο μέλη της τελευταίας εξίσωσης στη i
(update 14-8-11)
Προχτές έπεσε στα χέρια μου το βιβλίο "Φανταστικές ιστορίες, οι περιπέτειες της τετραγωνικής ρίζας του μείον 1", του Paul J. Nahin, εκδόσεις κάτοπτρο.
Ιδού λοιπόν μερικά ιστορικά στοιχεία που περιέχονται στο εκπληκτικό αυτό βιβλίο, σχετικά με τον υπολογισμό του ii:
Πολύ πριν το 1748, δηλαδή πολύ πριν ο Εuler διατυπώσει την ισότητα
Κάνουμε τώρα την αλλαγή μεταβλητής, u = ix.
Άρα x = -iu και, συνεπώς, dx = -idu.
Επομένως,
Το τελευταίο είναι γνωστό ολοκλήρωμα και περιέχεται, λόγου χάρη, σε τυπολόγια ολοκληρωμάτων. Συγκεκριμένα, βρίσκουμε:

Συνεπώς,
Αυτός ο ημιτελής υπολογισμός του ii δεν είναι ο πρώτος στην ιστορία. Το 1719, ο Ιταλός Giulio Carlo dei Toschi Fagnano (1682 – 1766) μελετώντας τον κύκλο έκανε έναν υπολογισμό παρόμοιο με εκείνον του Bernoulli. Μόνο που ο Fagnano εργάστηκε στην περίμετρο και όχι στο εμβαδόν του κύκλου. Γόνος μιας οικογένειας ευγενών η οποία ανέδειξε και έναν πάπα, ο Fagnano χρίστηκε κόμης το 1721 από τον Λουδοβίκο ΙΕ' και στη συνέχεια, το 1745, αναγορεύτηκε μαρκήσιος από τον πάπα Βεβέδικτο ΙΔ'. Υπήρξε μέλος τόσο της Βασιλικής Εταιρείας του Λονδίνου όσο και της Ακαδημίας Επιστημών του Βερολίνου, και έχαιρε εξαιρετικής φήμης σε όλη την Ευρώπη ως ιδιαίτερα δημιουργικός μαθηματικός.
O Fargano ξεκίνησε από τον μοναδιαίο κύκλο, παρατηρώνατς ότι το μήκος L ενός τόξου με επίκεντρη γωνία θ ισούται απλώς με θ
Στη συνέχεια επεξεργάστηκε αυτό το εξαιρετικά απλό ολοκλήρωμα, κάνοντάς το να μοιάζει πιο περίπλοκο … καταλήγοντας μετά από απλούς, αλλά ευφυείς υπολογισμούς στο ίδιο αποτέλεσμα με τον Bernoulli
Το 1921 ο Horace Scudder Uhler (1872 – 1956), φυσικός του Πανεπιστημίου Yale, δημοσίευσε την τιμή του ii με ακρίβεια μεγαλύτερη των πενήντα δεκαδικών ψηφίων. Ο καθηγητής Uhler δεν ασχολούνταν ερασιτεχνικά με τους υπολογισμούς. Οι υπολογισμοί ήταν το μεγάλο του πάθος της ζωής του. το 1947, για παράδειγμα, ενδιαφέρθηκε για τον μεγαλύτερο δυνατό δεκαδικό αριθμό που μπορεί να γραφεί χρησιμοποιώντας μόνο τρία 9. Πρόκειται για τον 999, και γνωρίζουμε ότι έχει 369693100 ψηφία. Υπολόγισε το λογάριθμο αυτού του «τέρατος» με ακτίβεια 250 δεκαδικών ψηφίων. Γιατί; Ισχυριζόταν ότι οι εν λόγω υπολογισμοί τον χαλαρώνουν, και νομίζω ότι πρέπει να τον πιστέψουμε.......
α i
όπου α ένας πραγματικός αριθμός και i η μονάδα των φανταστικών αριθμώνή "ακόμα χειρότερα" το
i i
Με ειλικρίνεια μου απάντησε πως δεν το γνωρίζει αλλά θα το ψάξει για να μου δώσει απάντηση την επόμενη ημέρα. Πράγματι την επομένη μου ανακοίνωσε ότι ψάχνοντας στα πανεπιστημιακά του βιβλία – τότε δεν υπήρχε internet! – το μόνο που βρήκε ήταν η εξίσωσηόπου e η βάση των νεπέριων λογαρίθμων, ο αριθμός e=2,718281828… που μεταξύ άλλων είναι και το όριο της ακολουθίας
όταν το ν τείνει στο άπειρο.
Θέτοντας x=π=3,14... παίρνουμεΤελικά η "γενική μορφή" της ομορφότερης εξίσωσης του κόσμου έλυσε όλες τις απορίες. Όσον αφορά το α i θα μπορούσε να γραφεί ως....
ή
Στην παραπάνω εξίσωση περιέχεται η μονάδα των πραγματικών αριθμών, η μονάδα των φανταστικών αριθμών, το μηδέν, ο αριθμός π και ο αριθμός e και γι’ αυτό θεωρείται ως η πιο όμορφη εξίσωση του κόσμου!
Όμως από που κι ως που ισχύει η εξίσωση;
Για έναν μαθητή λυκείου φαίνεται ακατανόητη ... αλλά γίνεται αμέσως κατανοητή διαμέσου των δυναμοσειρών, χρησιμοποιώντας τα παρακάτω αναπτύγματα
Τώρα είμαστε σε θέση να υπολογίσουμε και το i i
Το lni γράφεται
Οπότε:
και
Για κ=0 προκύπτει
i i = 0,207879...
Μπορούμε να επιβεβαιώσουμε τα παραπάνω χρησιμοποιώντας τον ιστότοπο www.wolframalpha.com. Γράφοντας απλά i i παίρνουμε το παρακάτω αποτέλεσμα
Ο "δεύτερος τρόπος"
Στα μαθηματικά υπάρχει πάντα και ο "δεύτερος" πιο απλός τρόπος!
Έτσι, για να υπολογίσουμε το i i , εργαζόμαστε ως εξής - ξεκινώντας από την πιο όμορφη εξίσωση του κόσμου:
Υψώνουμε και τα δυο μέλη της τελευταίας εξίσωσης στη i
και πολύ απλά προκύπτει ότι
......................................................................................................................(update 14-8-11)
Προχτές έπεσε στα χέρια μου το βιβλίο "Φανταστικές ιστορίες, οι περιπέτειες της τετραγωνικής ρίζας του μείον 1", του Paul J. Nahin, εκδόσεις κάτοπτρο.
Ιδού λοιπόν μερικά ιστορικά στοιχεία που περιέχονται στο εκπληκτικό αυτό βιβλίο, σχετικά με τον υπολογισμό του ii:
Πολύ πριν το 1748, δηλαδή πολύ πριν ο Εuler διατυπώσει την ισότητα
e±ix = cosx ± isinx
o υπολογισμός του ii είχε ήδη πραγματοποιηθεί με τη χρήση άλλων εξειδικευμένων και εξαιρετικά ευφυών μεθόδων. Έναν τέτοιο υπολογισμό αναφέρει και ο ίδιος ο Euler σε επιστολή του (με ημερομηνία 10 Δεκεμβρίου 1728) προς τον Jean Bernoulli. Με σύγχρονη ορολογία θα λέγαμε ότι ο Bernoulli θεώρησε τον κύκλο με κέντρο την αρχή των αξόνων και ακτίνα 1, δηλαδή τον κύκλο με εξίσωσηx2 + y2 = 1,
και στη συνέχεια σχημάτισε το ολοκλήρωμα για τον υπολογισμό του εμβαδού του πρώτου τεταρτημορίου του κύκλου. Πρόκειται για ένα κλασικό πλέον πρόβλημα που απαντά σε εισαγωγικά μαθήματα απειροστικού λογιμσμού. Αν συμβολίσουμε το εμβαδόν με Α (γνωρίσουμε βέβαια ότι ισούται με π/4), θα έχουμεΚάνουμε τώρα την αλλαγή μεταβλητής, u = ix.
Άρα x = -iu και, συνεπώς, dx = -idu.
Επομένως,
Το τελευταίο είναι γνωστό ολοκλήρωμα και περιέχεται, λόγου χάρη, σε τυπολόγια ολοκληρωμάτων. Συγκεκριμένα, βρίσκουμε:
Συνεπώς,
iln(i)=-π/2
όθεν προκύπτει άμεσα ότι, όπως πρινii=e-π/2
μολονότι ούτε ο Bernoulli ούτε ο Euler επιχείρησαν αυτό το τελευταίο βήμα.Αυτός ο ημιτελής υπολογισμός του ii δεν είναι ο πρώτος στην ιστορία. Το 1719, ο Ιταλός Giulio Carlo dei Toschi Fagnano (1682 – 1766) μελετώντας τον κύκλο έκανε έναν υπολογισμό παρόμοιο με εκείνον του Bernoulli. Μόνο που ο Fagnano εργάστηκε στην περίμετρο και όχι στο εμβαδόν του κύκλου. Γόνος μιας οικογένειας ευγενών η οποία ανέδειξε και έναν πάπα, ο Fagnano χρίστηκε κόμης το 1721 από τον Λουδοβίκο ΙΕ' και στη συνέχεια, το 1745, αναγορεύτηκε μαρκήσιος από τον πάπα Βεβέδικτο ΙΔ'. Υπήρξε μέλος τόσο της Βασιλικής Εταιρείας του Λονδίνου όσο και της Ακαδημίας Επιστημών του Βερολίνου, και έχαιρε εξαιρετικής φήμης σε όλη την Ευρώπη ως ιδιαίτερα δημιουργικός μαθηματικός.
O Fargano ξεκίνησε από τον μοναδιαίο κύκλο, παρατηρώνατς ότι το μήκος L ενός τόξου με επίκεντρη γωνία θ ισούται απλώς με θ
Στη συνέχεια επεξεργάστηκε αυτό το εξαιρετικά απλό ολοκλήρωμα, κάνοντάς το να μοιάζει πιο περίπλοκο … καταλήγοντας μετά από απλούς, αλλά ευφυείς υπολογισμούς στο ίδιο αποτέλεσμα με τον Bernoulli
iln(i)=-π/2
χωρίς να κάνει κι αυτός το τελευταίο βήμα που οδηγεί στο ii=e-π/2
.................................................Το 1921 ο Horace Scudder Uhler (1872 – 1956), φυσικός του Πανεπιστημίου Yale, δημοσίευσε την τιμή του ii με ακρίβεια μεγαλύτερη των πενήντα δεκαδικών ψηφίων. Ο καθηγητής Uhler δεν ασχολούνταν ερασιτεχνικά με τους υπολογισμούς. Οι υπολογισμοί ήταν το μεγάλο του πάθος της ζωής του. το 1947, για παράδειγμα, ενδιαφέρθηκε για τον μεγαλύτερο δυνατό δεκαδικό αριθμό που μπορεί να γραφεί χρησιμοποιώντας μόνο τρία 9. Πρόκειται για τον 999, και γνωρίζουμε ότι έχει 369693100 ψηφία. Υπολόγισε το λογάριθμο αυτού του «τέρατος» με ακτίβεια 250 δεκαδικών ψηφίων. Γιατί; Ισχυριζόταν ότι οι εν λόγω υπολογισμοί τον χαλαρώνουν, και νομίζω ότι πρέπει να τον πιστέψουμε.......

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου