H ΑΚΤΙΝΟΒΟΛΙΑ ΜΕΛΑΝΟΣ ΣΩΜΑΤΟΣ

ΠΕΡΙΕΧΟΜΕΝΑ
1. Εισαγωγή
2. Το μέλαν σώμα είναι το φωτεινότερο σώμα
3. Τα μεγέθη που περιγράφουν την ακτινοβολία του μέλανος σώματος
4. Η ερμηνεία της ακτινοβολίας του μέλανος σώματος
5. Η  απόδειξη του νόμου των Rayleigh – Jeans
6. Η απόδειξη του νόμου Planck
7. Η ακτινοβολία μέλανος σώματος σ’ ένα διαστελλόμενο σύμπαν

1. Εισαγωγή

Όταν ένα ηλεκτρομαγνητικό κύμα προσπίπτει στην επιφάνεια σώματος, ένα μέρος της ενέργειάς του απορροφάται, με αποτέλεσμα την αύξηση της εσωτερικής ενέργειας και της θερμοκρασίας του σώματος. Αντιστρόφως, ένα θερμό σώμα που δεν βρίσκεται σε επαφή με άλλα σώματα ή τον αέρα, ψύχεται, εκπέμποντας θερμική ενέργεια υπό μορφή ηλεκτρομαγνητικών κυμάτων.
Η θερμότητα δηλαδή μπορεί να διαδίδεται και στο κενό.
Ως θερμική ακτινοβολία θα θεωρούμε την ηλεκτρομαγνητική ακτινοβολία που εκπέμπουν τα σώματα εξαιτίας της θερμοκρασίας τους.
Πολλές φορές θεωρείται ότι η θερμική ακτινοβολία είναι μόνον η υπέρυθρη ακτινοβολία, που είναι εντελώς λάθος, διότι η θερμική ακτινοβολία μπορεί να αποτελείται από οποιοδήποτε μήκος κύματος.
Όταν ο ρυθμός με τον οποίο εκπέμπεται η θερμική ηλεκτρομαγνητική ακτινοβολία από ένα σώμα είναι ίσος με τον ρυθμό που απορροφάται και η θερμοκρασία του σώματος παραμένει σταθερή τότε μπορούμε να πούμε ότι το σώμα βρίσκεται σε θερμική ισορροπία με την ακτινοβολία.
Η πειραματική μελέτη της ακτινοβολίας που βρίσκεται σε ισορροπία με την ύλη γίνεται ως εξής:
Θεωρούμε το εσωτερικό μιας κοιλότητας ενός σώματος με σταθερή θερμοκρασία. Εξαιτίας της θερμικής κίνησης των φορτισμένων σωματιδίων του υλικού των τοιχωμάτων της κοιλότητας εκπέμπεται ηλεκτρομαγνητική ακτινοβολία.

Η παγιδευμένη στην κοιλότητα ακτινοβολία αλληλεπιδρά με τα φορτισμένα σωματίδια μεταβιβάζοντας σ’ αυτά ενέργεια. Όταν ο ρυθμός απορρόφησης ενέργειας από τα τοιχώματα είναι ίσος με τον ρυθμό εκπομπής, τότε έχει επιτευχθεί θερμική ισορροπία μεταξύ ύλης και ακτινοβολίας.
Ανοίγοντας μια οπή στην κοιλότητα, μικρή ως προς τις διαστάσεις της κοιλότητας, τότε η ακτινοβολία «ισορροπίας» που διαφεύγει δεν επηρεάζει την ισορροπία και μπορούμε να μελετήσουμε τις ιδιότητές της.
Για έναν εξωτερικό παρατηρητή η μικρή οπή εμφανίζεται ως επιφάνεια ενός απόλυτα μαύρου σώματος. Μια τέτοια επιφάνεια μπορεί να απορροφά και να εκπέμπει όλα τα μήκη κύματος του φάσματος της ηλεκτρομαγνητικής ακτινοβολίας. Για τον λόγο αυτό η ακτινοβολία που εξέρχεται από την κοιλότητα ονομάζεται ακτινοβολία μέλανος σώματος.
Η μελέτη του τρόπου με τον οποίο το ονομαζόμενο μέλαν σώμα εκπέμπει θερμική ακτινοβολία έπαιξε τεράστιο ρόλο στην εξέλιξη της φυσικής και σηματοδότησε την έναρξη της κβαντικής εποχής. 
Το αντίθετο του μέλανος σώματος προφανώς θα είναι το «λευκό». Όσο περισσότερη ακτινοβολία ανακλά ένα σώμα τόσο λιγότερη απορροφά, και τόσο πιο φωτεινό φαίνεται.
Θεωρούμε ένα σώμα φωτεινό όταν εκπέμπει αρκετή ακτινοβολία (στην ορατή ή οποιαδήποτε άλλη περιοχή του φάσματος). Όμως μπορεί κανείς να οδηγηθεί στο συμπέρασμα ότι το «μελανό» είναι και «σκοτεινό» και μάλιστα όσο πιο μελανό είναι ένα σώμα τόσο σκοτεινότερο είναι. Αυτό είναι τεράστιο λάθος.
Όπως θα δούμε στη συνέχεια το ιδανικό μέλαν σώμα είναι το φωτεινότερο όλων των σωμάτων.


2. Το μέλαν σώμα είναι το φωτεινότερο σώμα.

Η ανάλυση της σχέσης μεταξύ των ιδιοτήτων εκπομπής και απορρόφησης διαφόρων σωμάτων οδήγησε τον Kirchhoff σε ένα σημαντικό συμπέρασμα, γνωστό ως νόμος του Kirchhoff: όσο περισσότερη ακτινοβολία απορροφά ένα σώμα σε δεδομένη θερμοκρασία τόσο περισσότερη ακτινοβολία εκπέμπει. Δηλαδή, όσο πιο μελανό τόσο και πιο φωτεινό είναι. Για να εκφράσουμε μαθηματικά τον παραπάνω νόμο, πρέπει να ορίσουμε την απορροφητικότητα και την ένταση της εκπεμπόμενης ακτινοβολίας.
Η απορροφητικότητα (ή συντελεστής απορρόφησης) ενός σώματος, A_λ,Τ, για δεδομένο μήκος κύματος λ και δεδομένη απόλυτη θερμοκρασία Τ, είναι το κλάσμα της ισχύος που απορροφά το σώμα προς αυτήν που πέφτει πάνω του:

Ο συντελεστής απορρόφησης είναι καθαρός αριθμός, και για διάφορα σώματα παίρνει τιμές από 0 έως 1. Η τιμή του είναι 0 για το απολύτως λευκό σώμα (ή για τον τέλειο ανακλαστήρα - το ιδανικό κάτοπτρο. Η απολύτως λευκή επιφάνεια διαχέει ομοιογενώς προς όλες τις κατευθύνσεις τις προσπίπτουσες ακτίνες, ενώ το ιδανικό κάτοπτρο τις ανακλά σε κατεύθυνση που προσδιορίζεται από τη γωνία πρόσπτωσης) και 1 για το ιδανικό μέλαν σώμα.
Η συνάρτηση φασματικής κατανομής της αφετικής ικανότητας Ι_λ,Τ ή η ένταση της ακτινοβολίας που εκπέμπει ένα σώμα με μήκη κύματος μεταξύ λ και λ+Δλ και δεδομένη απόλυτη θερμοκρασία Τ, είναι η ισχύς που εκπέμπει η μονάδα επιφάνειας του σώματος ανά Δλ στην περιοχή πλησίον του λ:

Έστω ότι διαθέτουμε ένα πλήθος σωμάτων με διαφορετική απορροφητικότητα A_λ,Τ (μεταξύ των σωμάτων αυτών το ιδανικό μέλαν σώμα και το ιδανικό λευκό σώμα). Θερμαίνουμε τα σώματα στην ίδια θερμοκρασία Τ.
Τότε σύμφωνα με το νόμο του Kirchhoff, τα σώματα δεν θα εκπέμπουν την ίδια ακτινοβολία: το φωτεινότερο θα είναι το ιδανικό μέλαν σώμα, ενώ το ιδανικό λευκό σώμα θα είναι απολύτως σκοτεινό. Μπορούμε για το ιδανικό μέλαν σώμα να συμβολίσουμε την απορροφητικότητα και την ένταση εκπομπής με ιδιαίτερα σύμβολα:

Είναι σημαντικό ότι το ιδανικό μέλαν σώμα όχι μόνο εκπέμπει τη μέγιστη ακτινοβολία σε δεδομένη θερμοκρασία, αλλά επιπλέον χαρακτηρίζεται από μια αυστηρά καθορισμένη φασματική σύνθεση. Με άλλα λόγια , η i_λ,Τ είναι μια οικουμενική συνάρτηση των λ και Τ. Σύμφωνα με τα παραπάνω, ο νόμος του Kirchhoff μπορεί να γραφεί ως εξής:

Έγιναν πολλές προσπάθειες για να υπολογιστεί η συνάρτηση i_λ,Τ θεωρητικά. Τελικά, όπως θα δούμε στη συνέχεια, το κατάφερε ο Max Planck, το 1900:

όπου c η ταχύτητα του φωτός στο κενό, k η σταθερά Boltzmann και h η σταθερά Planck.
Όταν η θερμοκρασία T ενός σώματος διατηρείται σταθερή, τα μεγέθη A, I και i εξαρτώνται μόνον από το μήκος κύματος λ, οπότε μπορούμε να τα συμβολίζουμε με Α_λ και i_λ.
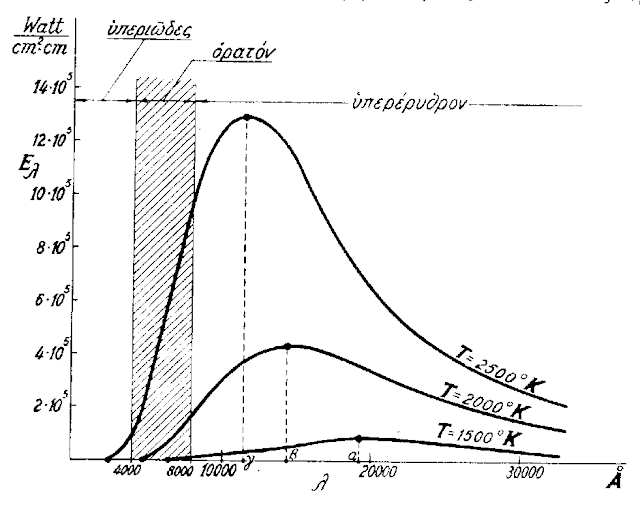
Στο παρακάτω σχήμα φαίνεται η γραφική παράσταση της συνάρτησης του Planck για δυο θερμοκρασίες Τ₁=2000Κ, Τ₂=3000Κ.

Παρόμοιο (σε διαφορετική κλίμακα) είναι και το επόμενο σχήμα....

3. Τα μεγέθη που περιγράφουν την ακτινοβολία του μέλανος σώματος.

Με κατάλληλες συσκευές (φασματοσκόπια) μπορούμε να προσδιορίσουμε τις ιδιότητες της ακτινοβολίας που εξέρχεται από την οπή. Μεγάλη σύγχυση προκαλούν οι συναρτήσεις που περιγράφουν την ακτινοβολία του μέλανος σώματος. Ας ξεκαθαρίσουμε λίγο την κατάσταση.
Παραπάνω χρησιμοποιήθηκε η συνάρτηση φασματικής κατανομής της αφετικής ικανότητας Ι(λ,Τ)[≡ i_λ,T] ή η ένταση της ακτινοβολίας που εκπέμπει ένα σώμα με μήκη κύματος μεταξύ λ και λ+Δλ και δεδομένη απόλυτη θερμοκρασία Τ, που είναι η ισχύς που εκπέμπει η μονάδα επιφάνειας του σώματος ανά Δλ στην περιοχή πλησίον του λ:

Μονάδα μέτρησής της είναι το 1W/m³. Πολλές φορές το παραπάνω μέγεθος εμφανίζεται χωρίς τον παράγοντα π στον αριθμητή, ως

και στις μονάδες μέτρησης αναφέρεται και το steradian (που δεν είναι μονάδα φυσικού μεγέθους), δηλ. 1W/m³sr
Αν το παραπάνω μέγεθος εκφραστεί συναρτήσει της συχνότητας τότε έχουμε

με μονάδα μέτρησης 1W.s/m²=1J/ m².
Γενικά ισχύει:

Το μέγεθος όμως που χρησιμοποιούμε συνήθως στην θεωρητική περιγραφή της ακτινοβολίας του μέλανος σώματος, είναι η φασματική κατανομή ενεργειακής πυκνότητας u(f,T), που έχει μονάδες J/m³.Hz =1J.s/m³
Μπορεί να γραφεί συναρτήσει του μεγέθους I(f,T) που έχει μονάδες J/m², ως

[Η απόδειξη της σχέσης u = 4πΙ/c , γίνεται χρησιμοποιώντας γεωμετρική οπτική]
Έτσι προσδιορίζεται η πυκνότητα ενέργειας των Η.Μ. κυμάτων στην κοιλότητα [ε=E/V] σε κάθε διάστημα συχνοτήτων από f έως f+df. Η φασματική κατανομή ενεργειακής πυκνότητας ορίζεται ως

όπου Δε η πυκνότητα ενέργειας των Η.Μ. κυμάτων των οποίων οι συχνότητες παίρνουν τιμές από f  έως  f + df.
Η φασματική κατανομή συναρτήσει της συχνότητας φαίνεται στην γραφική παράσταση του σχήματος.

Αν μεταβάλλουμε τη θερμοκρασία Τ τότε προσδιορίζεται μια διαφορετική καμπύλη. Από την μελέτη των πειραματικών καμπυλών προκύπτουν οι εξής παρατηρήσεις:
1. Η καμπύλη της φασματικής κατανομής u(f,T) είναι συνεχής και η μορφή της εξαρτάται μόνο από τη θερμοκρασία T. Είναι ανεξάρτητη από τον όγκο, το σχήμα και κυρίως από το υλικό των τοιχωμάτων. Αυτό το έδειξε ο Kirchhoff το 1859.
2. Για τις πολύ μικρές και τις πολύ μεγάλες συχνότητες η τιμή της φασματικής κατανομής η τιμή της φασματικής κατανομής u(f,T) τείνει στο μηδέν. Για κάθε θερμοκρασία προκύπτει διαφορετική συνεχής καμπύλη. Κάθε καμπύλη εμφανίζει μέγιστο σε μια συχνότητα f_max. Η συχνότητα που αντιστοιχεί στο μέγιστο της καμπύλης αυξάνεται καθώς αυξάνει η θερμοκρασία

f_max = (σταθ.)Τ

Αυτός είναι ο νόμος μετατόπισης του Wien. H τιμή της σταθεράς είναι ανεξάρτητη από το υλικό των τοιχωμάτων και το σχήμα της κοιλότητας.
3. Το εμβαδόν κάτω από τη γραφική παράσταση της u(f,T) είναι ανάλογο του Τ⁴. Το εμβαδόν εκφράζει την πυκνότητα ενέργειας της κοιλότητας διότι

Έτσι,

ε = σ Τ⁴

Αυτός είναι ο νόμος των Stefan – Boltzmann. H τιμή της σταθεράς σ είναι ανεξάρτητη από το υλικό και το σχήμα των τοιχωμάτων της κοιλότητας.
Το γεγονός ότι η καμπύλη u(f,T), το «φάσμα του μέλανος σώματος» είναι ανεξάρτητη από το υλικό, σε αντίθεση με τα γραμμικά φάσματα των αερίων ή τα συνεχή φάσματα μη μελανών σωμάτων, δείχνει ότι μπορεί να ερμηνευθεί χωρίς καμία αναφορά στην ατομική δομή της ύλης.


4. Η ερμηνεία της ακτινοβολίας του μέλανος σώματος.

Οι Rayleigh – Jeans προσπάθησαν να εξηγήσουν την ακτινοβολία του μέλανος σώματος σύμφωνα με την κλασσική μηχανική και την Η.Μ. θεωρία του Maxwell. Θεωρώντας στάσιμα Η.Μ. κύματα στην κοιλότητα του πρότυπου μέλανος σώματος και ότι το υλικό των τοιχωμάτων, που συνίσταται από φορτισμένους αρμονικούς ταλαντωτές, ανταλλάσσει οποιοδήποτε ποσό ενέργειας με τα Η.Μ. κύματα, υπολόγισαν την έκφραση:

Όπως φαίνεται και στο σχήμα η αποτυχία είναι παταγώδης.

Η σχέση των Rayleigh – Jeans μπορεί να αποδειχθεί με διαστατικά επιχειρήματα. Αν υποθέσουμε ότι το μέγεθος u(f,T) εξαρτάται εκτός από τη συχνότητα f και τη θερμοκρασία T, από την ταχύτητα του φωτός c και την σταθερά Boltzmann k, τότε

u~f^x c^y k^z T^ω

Τοποθετώντας στο πρώτο και στο δεύτερο μέλος τις αντίστοιχες μονάδες μέτρησης προκύπτει

J s m^-3=s^-x-ym^yJ^zK^-z+ω

Έτσι προκύπτει το σύστημα

Οπότε

Απουσιάζει μόνο ο αριθμητικός παράγοντας 8π.
Στην κανονική απόδειξη του νόμου το ζητούμενο είναι να υπολογιστούν οι δυνατοί κανονικοί τρόποι ταλάντωσης των στάσιμων Η.Μ. κυμάτων μέσα στην κοιλότητα. Σε έναν κανονικό τρόπο ταλάντωσης όλα τα μέρη του συστήματος ταλαντώνονται με την ίδια κανονική συχνότητα.
Όπως στα στάσιμα κύματα σε μονοδιάστατη χορδή μήκους ℓ με ακίνητα άκρα. Για κάθε συχνότητα f=nc/2ℓ ή μήκος κύματος λ=2ℓ/n (όπου n ακέραιος) έχουμε και έναν διαφορετικό κανονικό τρόπο ταλάντωσης.
Κάθε διαφορετικός τρόπος ταλάντωσης του συστήματος ισοδυναμεί με έναν βαθμό ελευθερίας του συστήματος. Βαθμοί ελευθερίας ενός συστήματος είναι οι ανεξάρτητοι τρόποι με τους οποίους ένα σύστημα μπορεί να αποκτήσει ενέργεια. Οι δυνατοί κανονικοί τρόποι ταλάντωσης στην περιοχή συχνοτήτων (f, f+df) ανά μονάδα όγκου υπολογίζονται ότι είναι

8πf²/c³

Σύμφωνα με το θεώρημα ισοκατανομής ενέργειας σε κάθε τρόπο ταλάντωσης ή σε κάθε βαθμό ελευθερίας αντιστοιχούμε μια μέση ενέργεια

(Στην πραγματικότητα σε κάθε βαθμό ελευθερίας αντιστοιχούμε ενέργεια kT/2, όμως όπως θα δούμε στην κανονική απόδειξη το ηλεκτρομαγνητικό κύμα γενικά έχει δυο βαθμούς ελευθερίας, οπότε αντιστοιχούμε ενέργεια 2kT/2=kT). Έτσι

παίρνοντας μια πρώτη ιδέα για το πώς προκύπτει ο νόμος Rayleigh – Jeans.
To ότι ο νόμος αυτός πάσχει όχι μόνο πειραματικά αλλά και θεωρητικά φαίνεται αμέσως, δεδομένου ότι το σύνολο των βαθμών ελευθερίας ενός Η.Μ. πεδίου μέσα σε μια κοιλότητα είναι προφανώς άπειρο, διότι έχουμε άπειρο αριθμό δυνατών στάσιμων κυμάτων (όπως και σε μια χορδή έχουμε άπειρο αριθμό μονοδιάστατων στάσιμων κυμάτων).

Το 1900 ο M. Planck στην προσπάθειά του να ερμηνεύσει το φάσμα του μέλανος σώματος, έκανε μια υπόθεση έξω από κάθε λογική για τη φυσική της εποχής του. Το γεγονός ότι ο νόμος αυτός πάσχει όχι μόνο πειραματικά αλλά και θεωρητικά φαίνεται αμέσως, δεδομένου ότι το σύνολο των βαθμών ελευθερίας ενός Η.Μ. πεδίου μέσα σε κοιλότητα είναι προφανώς άπειρο, διότι έχουμε άπειρο αριθμό δυνατών στάσιμων κυμάτων (όπως σε μια χορδή έχουμε άπειρο αριθμό μονοδιάστατων κυμάτων).

Υπόθεση Planck: Ένας ταλαντωτής με ιδιοσυχνότητα f μπορεί να προσλάβει ή να αποδώσει ενέργεια μόνο κατά ποσότητες:

E = n h f

όπου n ακέραιος αριθμός και h θεμελιώδης σταθερά της φύσης.
Τα σωματίδια των τοιχωμάτων (που φέρουν φορτίο) είναι αρμονικοί ταλαντωτές με συγκεκριμένες ιδιοσυχνότητες f. Τα Η.Μ. κύματα που γεμίζουν την κοιλότητα δεν μπορούν να ανταλλάξουν οποιοδήποτε ποσό ενέργειας με τους ταλαντωτές, παρά μόνον σε διάκριτα (ασυνεχή) ποσά ενέργειας.
Έτσι γεννήθηκε η κβαντική φυσική, σύμφωνα με την οποία το φως άλλοτε συμπεριφέρεται ως Η.Μ. κύμα και άλλοτε ως σωματίδια, τα φωτόνια.
Η βασική διαφορά στις αποδείξεις των νόμων Planck και Rayleigh – Jeans είναι στην μέση ενέργεια που αντιστοιχούμε σε κάθε βαθμό ελευθερίας. Για να πάρουμε μια ιδέα της λογικής που χαρακτηρίζει τον νόμο Planck,
συμβολίζουμε
με N₀ τους ταλαντωτές που έχουν ενέργεια E₀=0,
με N₁ τους ταλαντωτές με ενέργεια E₁=hf,
με N₂ τους ταλαντωτές με E₂=2hf
κ.ο.κ.
Θεωρούμε (χωρίς πολλές συζητήσεις!) ότι σύμφωνα με την κβαντομηχανική λογική θα ισχύουν:

Έτσι, ο συνολικός αριθμός ταλαντωτών είναι

και η συνολική ενέργεια των ταλαντωτών

Συνεπώς η ζητούμενη μέση ενέργεια (το αντίστοιχο του

στον νόμου Rayleigh – Jeans) θα είναι

Όμως έχουμε

και με περισσότερη σκέψη

οπότε

Όπως στον νόμο Rayleigh – Jeans, έτσι και τώρα θα έχουμε

8πf²/kT

κανονικούς τρόπους ταλάντωσης.
Στον νόμο Planck η ακριβής μορφή της φασματικής κατανομής u(f ,T) που συμφωνεί τέλεια με τα πειραματικά δεδομένα είναι:

Παρατηρούμε ότι όταν το hf  είναι πολύ μικρότερο του kT ισχύει

προκύπτει δηλαδή ο νόμος Rayleigh – Jeans.
Πολλές φορές ο νόμος Planck γράφεται συναρτήσει του μήκους κύματος ως

5.  Η απόδειξη του νόμου των Rayleigh – Jeans

 

6. Η απόδειξη του νόμου Planck

 

7. Η ακτινοβολία μέλανος σώματος σ’ ένα διαστελλόμενο σύμπαν

BΙΒΛΙΟΓΡΑΦΙΑ
1. The Feynman Lectures on Physics
2. "Thermodynamics and Statistical Mechanics", Arnold Sommerfeld
3. "Στατιστική Φυσική", Ι. Δ. Βέργαδος, Η. Σ. Τριανταφυλλόπουλος
4. "Στατιστική Φυσική", F. Mandl
5. "Γενική Φυσική", Κ. Δ. Αλεξόπουλος
6. "Φυσική των Ταλαντώσεων και των Κυμάτων", H. J. Pain
7. "Τα τρία πρώτα λεπτά", Steven Weinberg 
...........................