Άραγε πρέπει να γνωρίζουμε τα μυστικά της κβαντομηχανικής για να εκτιμήσουμε το μέγεθος των ατόμων; Πρέπει να επιλύσουμε την τρισδιάστατη εξίσωση του Schrödinger για το άτομο του υδρογόνου ώστε να υπολογίσουμε την ακτίνα του; Όχι απαραίτητα!
Μπορούμε χρησιμοποιώντας τις τιμές μερικών σταθερών της Φυσικής και τις αντίστοιχες μονάδες τους να υπολογίσουμε με ακρίβεια την ακτίνα του ατόμου του υδρογόνου r0, την επονομαζόμενη ακτίνα Bohr.
Πίσω από τις μεγάλες επιστημονικές ανακαλύψεις πολλές φορές βρίσκονται πάρα πολύ απλές σκέψεις. Ο Νiels Bohr γνωρίζοντας ότι το άτομο του υδρογόνου αποτελείται από ένα πρωτόνιο και ένα ηλεκτρόνιο τα οποία φέρουν ηλεκτρικό φορτίο e και αλληλεπιδρούν ηλεκτροστατικά υπέθεσε ότι η ακτίνα του ατόμου θα εξαρτάται οπωσδήποτε από το φορτίο e, τη σταθερά που υπεισέρχεται στο νόμο της ηλεκτροστατικής έλξης Coulomb kC και την μάζα του ηλεκτρονίου me.
Υπέθεσε επιπλέον ότι και η σταθερά του Planck
πρέπει να παίζει ρόλο στα ατομικά φαινόμενα (η σταθερά του Planck που είχε εισαχθεί κάποια χρόνια πριν, από τον Max Planck, για την ερμηνεία της ακτινοβολίας του μέλανος σώματος). Ίσως να μην απέκλεισε και την ταχύτητα του φωτός c που αποτελεί μια σταθερά της κλασικής φυσικής.
Το ζητούμενο για τον Bohr ήταν το πως πρέπει να συνδυαστούν οι παραπάνω σταθερές έτσι ώστε να μας δώσουν ένα μέγεθος με μονάδες μήκους.
Ο μοναδικός συνδυασμός που προκύπτει (και δεν περιέχει τελικά την ταχύτητα του φωτός) δίνεται από την παρακάτω εξίσωση
Θέτοντας τις παρακάτω τιμές των σταθερών
προκύπτει ότι η ακτίνα του ατόμου είναι
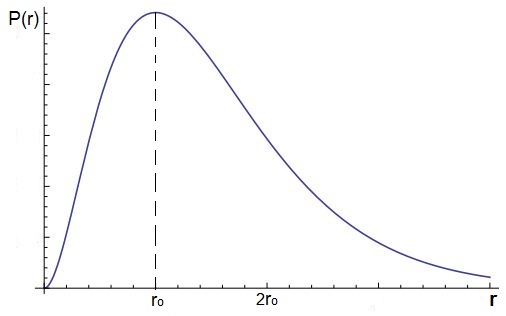
Η ακτινική πυκνότητα πιθανότητας στη θεμελιώδη κατάσταση του ατόμου του υδρογόνου – που προκύπτει επιλύοντας την εξίσωση Schrödinger – φαίνεται στο παρακάτω σχήμα. Η πιθανότερη απόσταση του ηλεκτρονίου από τον πυρήνα ταυτίζεται με την ακτίνα Bohr.
Επειδή μερικοί θα προβληματίζονται για το πώς ακριβώς φθάνουμε στην εξίσωση της ακτίνας
παραθέτουμε στη συνέχεια λίγα απλά μαθηματικά....
Μπορούμε να καταλήξουμε στην παραπάνω εξίσωση γράφοντας
Σκοπός μας είναι να υπολογίσουμε τους άγνωστους εκθέτες:
και το σύστημα των εξισώσεων για κάθε μονάδα μέτρησης
Λύνοντας το παραπάνω σύστημα παίρνουμε τελικά
Η παραπάνω απλοποιημένη μορφή της διαστατικής ανάλυσης μπορεί να εφαρμοστεί με επιτυχία για τον προσδιορισμό διαφόρων μεγεθών της φυσικής (π.χ. δείτε ΕΔΩ πως υπολογίζεται η συχνότητα ταλάντωσης του αρμονικού ταλαντωτή)
Μπορούμε χρησιμοποιώντας τις τιμές μερικών σταθερών της Φυσικής και τις αντίστοιχες μονάδες τους να υπολογίσουμε με ακρίβεια την ακτίνα του ατόμου του υδρογόνου r0, την επονομαζόμενη ακτίνα Bohr.
Πίσω από τις μεγάλες επιστημονικές ανακαλύψεις πολλές φορές βρίσκονται πάρα πολύ απλές σκέψεις. Ο Νiels Bohr γνωρίζοντας ότι το άτομο του υδρογόνου αποτελείται από ένα πρωτόνιο και ένα ηλεκτρόνιο τα οποία φέρουν ηλεκτρικό φορτίο e και αλληλεπιδρούν ηλεκτροστατικά υπέθεσε ότι η ακτίνα του ατόμου θα εξαρτάται οπωσδήποτε από το φορτίο e, τη σταθερά που υπεισέρχεται στο νόμο της ηλεκτροστατικής έλξης Coulomb kC και την μάζα του ηλεκτρονίου me.
Υπέθεσε επιπλέον ότι και η σταθερά του Planck
πρέπει να παίζει ρόλο στα ατομικά φαινόμενα (η σταθερά του Planck που είχε εισαχθεί κάποια χρόνια πριν, από τον Max Planck, για την ερμηνεία της ακτινοβολίας του μέλανος σώματος). Ίσως να μην απέκλεισε και την ταχύτητα του φωτός c που αποτελεί μια σταθερά της κλασικής φυσικής.
Το ζητούμενο για τον Bohr ήταν το πως πρέπει να συνδυαστούν οι παραπάνω σταθερές έτσι ώστε να μας δώσουν ένα μέγεθος με μονάδες μήκους.
Ο μοναδικός συνδυασμός που προκύπτει (και δεν περιέχει τελικά την ταχύτητα του φωτός) δίνεται από την παρακάτω εξίσωση
Θέτοντας τις παρακάτω τιμές των σταθερών
προκύπτει ότι η ακτίνα του ατόμου είναι
ή 0,5 Angstrom
Η τιμή αυτή αντιστοιχεί στην ακτίνα της πρώτης τροχιάς του Bohr στο άτομο του υδρογόνου, στην παλιά κβαντική θεωρία.Η ακτινική πυκνότητα πιθανότητας στη θεμελιώδη κατάσταση του ατόμου του υδρογόνου – που προκύπτει επιλύοντας την εξίσωση Schrödinger – φαίνεται στο παρακάτω σχήμα. Η πιθανότερη απόσταση του ηλεκτρονίου από τον πυρήνα ταυτίζεται με την ακτίνα Bohr.
Επειδή μερικοί θα προβληματίζονται για το πώς ακριβώς φθάνουμε στην εξίσωση της ακτίνας
παραθέτουμε στη συνέχεια λίγα απλά μαθηματικά....
Μπορούμε να καταλήξουμε στην παραπάνω εξίσωση γράφοντας
Σκοπός μας είναι να υπολογίσουμε τους άγνωστους εκθέτες:
α, β, γ, δ και ε.
Απαιτούμε η τελευταία εξίσωση να ικανοποιείται από τις μονάδες μέτρησης των μεγεθών που περιέχονται στο πρώτο και δεύτερο μέλος. Αντικαθιστώντας τις μονάδες μέτρησης προκύπτεικαι το σύστημα των εξισώσεων για κάθε μονάδα μέτρησης
Λύνοντας το παραπάνω σύστημα παίρνουμε τελικά
Η παραπάνω απλοποιημένη μορφή της διαστατικής ανάλυσης μπορεί να εφαρμοστεί με επιτυχία για τον προσδιορισμό διαφόρων μεγεθών της φυσικής (π.χ. δείτε ΕΔΩ πως υπολογίζεται η συχνότητα ταλάντωσης του αρμονικού ταλαντωτή)









Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου