Για να απαντηθεί ο γρίφος που παρουσιάστηκε ΕΔΩ απαιτείται μια ιδιαίτερα πολύπλοκη λογική. Ας θυμηθούμε τον γρίφο:
Δυο μαθηματικοί - ο Γ. και ο Α. - συνελήφθησαν από μια φυλή ανθρωποφάγων. Όταν τους παρουσίασαν στον αρχηγό της φυλής με έκπληξη διαπίστωσαν ότι αυτός ήταν απόφοιτος της φυσικομαθηματικής σχολής του πανεπιστημίου Αθηνών και λάτρης των μαθηματικών. Γι αυτό τους έδωσε μια ευκαιρία για να γλιτώσουν, αρκεί να έλυναν το πρόβλημα που θα τους έθετε. Τους είπε:
"Έχω σκεφτεί δυο ακέραιους και θετικούς αριθμούς χ και ψ. Θα αποκαλύψω τώρα στον Γ, κρυφά από τον Α, το γινόμενο (p0=χ·ψ) αυτών των αριθμών.
Και μετά θα πω στον Α, κρυφά από τον Γ, το άθροισμά τους (s0=χ+ψ)."
(Το άθροισμά των αριθμών είναι είναι μικρότερο του 100 και είναι διαφορετικοί από τη μονάδα).
Στη συνέχεια ζήτησε από τους δυο μαθηματικούς να βρουν τους αριθμούς.
Ακολούθησε ο παρακάτω διάλογος μεταξύ των μαθηματικών Γ και Α
Γ: "Απ' ότι φαίνεται δεν μπορώ να βρω τους αριθμούς" (γ1)
Α: "Το ήξερα ότι δεν θα τους βρεις!" (α1)
Γ: "Αφού είναι έτσι τώρα τους βρήκα!" (γ2)
Α: "Τώρα τους βρήκα και εγώ!" (α2)
Μπορούμε από τον παραπάνω διάλογο να βρούμε ποιοι είναι οι αριθμοί;
Με μια πρώτη ματιά αυτό φαίνεται αδύνατον ! Πως μπορούμε να βρούμε τους αριθμούς όταν δεν έχει δοθεί καμία πληροφορία γι αυτούς; Κι όμως μπορούμε !
Υποθέτουμε –χωρίς να βλάπτεται η γενικότητα – ότι χ≤ψ.
Ένας τρόπος να βρούμε τους αριθμούς είναι η μέθοδος της δοκιμής και του λάθους:
να ελέγξουμε όλα τα ζεύγη των αριθμών που ικανοποιούν τις συνθήκες
Η εικασία των Goldbach - Euler
Ποιες πληροφορίες μπορούμε να εξαγάγουμε από τις προτάσεις (γ1) και (α1);
Η πρώτη πρόταση μας λέει ότι το p0 (= χ·ψ) δεν παραγοντοποιείται μονοσήμαντα σε γινόμενο δυο αριθμών που ικανοποιούν τις ανισότητες (1) και (2). (πρόταση γ11)
Η δεύτερη πρόταση σημαίνει ότι με όποιον τρόπο κι αν αναλύσουμε το s0 σε άθροισμα δυο αριθμών που ικανοποιούν την ανισότητα (1), το γινόμενο των προσθετέων θα έχει την ιδιότητα γ11. (πρόταση α11)
Η πρώτη συνθήκη εξαιρεί μερικά γινόμενα, η δεύτερη αποκλείει ορισμένα αθροίσματα. Ειδικά από την (α11) έπεται ότι είναι αδύνατον να παρασταθεί το s0 ως άθροισμα δυο πρώτων. (Διαφορερικά το γινόμενο αυτών των πρώτων έχει μια και μοναδική παραγοντοποίηση σε δυο παράγοντες που ικανοποιούν τις ανισότητες (1) και (2) και επομένως δεν ικανοποιεί την (γ11)).
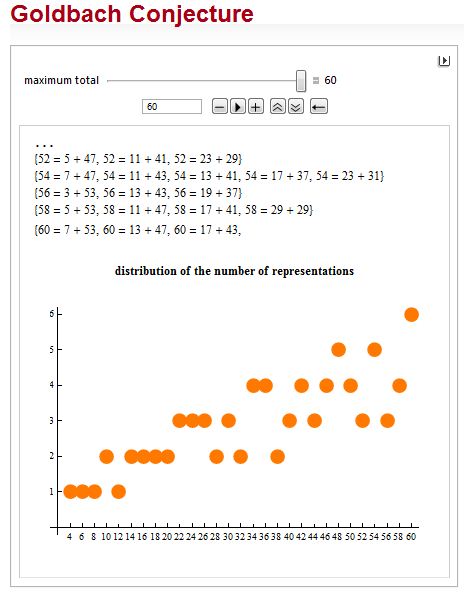
Κάθε άρτιος αριθμός, όμως που ικανοποιεί την ανισότητα (2) γράφεται ως άθροισμα δυο πρώτων (αυτό μπορούμε να το πιστοποιήσουμε άμεσα για όλους τους αριθμούς
To επιχείρημα....
που χρησιμοποιήσαμε παραπάνω – ότι όλοι οι άρτιοι αριθμοί από το 4 έως το 98 μπορούν να γραφούν ως άθροισμα δυο πρώτων – συνδέεται με ένα συναρπαστικό μαθηματικό πρόβλημα. Το 1972, ένα μέλος της Ακαδημίας των Επιστημών της Αγίας Πετρούπολης, ο Christian Goldbach (Γερμανός που προσέφερε τις υπηρεσίες του στο ρωσικό κράτος) έστειλε μια επιστολή στον Leonard Euler στην οποία διατύπωνε την εικασία ότι κάθε περιττός αριθμός μεγαλύτερος του 5 μπορεί να παρασταθεί ως άθροισμα τριών πρώτων. Ο Euler στην απάντησή του πρότεινε την εικασία ότι κάθε άρτιος αριθμός μεγαλύτερος του 2 γράφεται ως άθροισμα δυο πρώτων. (Δεν είναι δύσκολο να συναγάγουμε την εικασία του Goldbach από την υπόθεση Euler – δοκιμάστε το μόνοι σας!).
Και οι δυο εικασίες για δυο σχεδόν αιώνες, φαινόταν αδύνατον να αποδειχθούν, παρότι είχαν επαληθευτεί με άμεση έρευνα για όλους τους αριθμούς έως το 9.000.000.
Το 1930, ο σπουδαίος ρώσος μαθηματικός L.G. Shnirelman απέδειξε ότι υπάρχει ένας αριθμός k τέτοιος ώστε κάθε ακέραιος n>1 να παρίσταται ως άθροισμα k το πολύ πρώτων αριθμών. Στην απόδειξη του Shnirelman ο αριθμός k ήταν μάλλον μεγάλος. Αργότερα αποδείχθηκε ότι το θεώρημα αληθεύει για k=20.
Το 1934, ένας άλλος διάσημος ρώσος μαθηματικός, ο I. M. Vinogradov, απέδειξε ότι κάθε αριθμός n>n0, για κάποιο συγκεκριμένο n0, γράφεται ως άθροισμα τριών πρώτων. Η σταθερά του Vinogradov είναι πολύ μεγάλος αριθμός
Όσον αφορά την εικασία του Εuler δεν έχει επιτευχθεί κάποια σημαντική πρόοδος προς την κατεύθυνση της απόδειξής της. (διαβαστε περισσότερα ΕΔΩ)
Δεύτερος γύρος
Μπορούμε να μειώσουμε κι άλλο το πλήθος των υποψήφιων για το s0: μπορούμε να συμπεράνουμε από την πρόταση (α11) ότι
Μετά την απόδειξη της ανισότητας (3), το πλήθος των δυνατών τιμών του s0 μειώνεται σε έντεκα:
Αυτό το a δεν μπορεί να ισούται με τη μονάδα, διότι υπάρχουν τουλάχιστον δυο παραγοντοποιήσεις του 2m. Πράγματι, ας υποθέσουμε ότι a=1. Τότε, ο αριθμός m είναι σύνθετος, οπότε μπορούμε να γράψουμε m=uv, όπου u>2 και v>2, ενώ και οι δυο παραγοντοποιήσεις
"Τώρα τους βρήκα και εγώ!"
Τέλος, ας χρησιμοποιήσουμε τις προτάσεις (γ2) και (α2). Θα μπορούσαμε να τις ερμηνεύσουμε όπως τις δυο προηγούμενες. Υπάρχει όμως ένας συντομότερος τρόπος. Από την (α2) και την ανισότητα (3): s0<55, συμπεραίνουμε ότι s0<33 (5) Ας υποθέσουμε ότι αυτό δεν αληθεύει. Τότε, s0≥33, και ο μαθηματικός Α, αναλύοντας το s0 σε άθροισμα δυο όρων με κάθε δυνατό τρόπο, θα έβρισκε τις εξής παραλλαγές: s0=(s0-31)+31=(s0-29)+29 Η πορεία των σκέψεών του θα ήταν τότε η εξής: αν είχε δοθεί στον Γ το γινόμενο (s0-31)·31, τότε, αν χρησιμοποιούσε την εκτίμηση (3): s0<55 και το γεγονός ότι ο 31 είναι πρώτος αριθμός, θα είχε καταλάβει ότι το (s0-31)·31 έχει μόνο μια παραγοντοποίηση τέτοια ώστε το άθροισμα των δυο πρώτων όρων της να ικανοποιεί την ανισότητα (3). Τότε ο Γ θα μάντευε τους άγνωστους αριθμούς. Το ίδιο επιχείρημα, όμως, εφαρμόζεται και στο γινόμενο (s0-29)·29. Επομένως, στην περίπτωση s0≥33, o μαθηματικός Α δεν θα μπορούσε να προσδιορίσει ακριβώς τους αριθμούς χ και ψ ακόμη και μετά τη δήλωση του (γ2) του Γ, αντίθετα απ' ό,τι συνέβη στην ιστορία μας. Άρα η ανισότητα (5): s0<33 είναι πραγματικά αληθής, και έτσι απομένουν μόνο πέντε αριθμοί:
όπου p περιττός πρώτος και n>1, τότε ο Γ μπορεί να προσδιορίσει με βεβαιότητα τους μυστικούς αριθμούς, διότι υπάρχει μόνο ένα περιττό άθροισμα της μορφής
συγκεκριμένα, το
Έτσι, αν το s0 έχει δυο αναπαραστάσεις της μορφής
τότε ο Α δεν μπορεί να βρει την απάντηση και να κάνει τη δήλωση (α2). Αυτή η παρατήρηση εξαιρεί τρεις ακόμη αριθμούς, τους
Τώρα τους βρήκαμε κι εμείς !
Στην περίπτωση του αριθμού s0=29, το τελευταίο επιχείρημα δεν ισχύει, διότι υπάρχει μόνο μια αναπαράσταση της μορφής
με p περιττό πρώτο (29=16+13). Μπορούμε, όμως, να το χρησιμοποιήσουμε ελαφρά τροποποιημένο για την ανάλυση: 29=4+25. Στην περίπτωση p0=4·25 έχουμε μόνο ένα ακόμη δυνατό περιττό άθροισμα εκτός από το 29, το 25=20+5 (προφανώς 4·25=5·35), αλλά τότε το 25-2 είναι πρώτος, ενώ το s0-2 πρέπει να είναι σύνθετος. Έτσι, σ' αυτή την περίπτωση είναι και πάλι αδύνατον να μαντέψει ο Α τους αριθμούς, συνεπώς η λίστα των υποψηφίων περιορίζεται σε έναν αριθμό, τον 17 – δηλαδή, είτε s0=17 είτε το πρόβλημα δεν έχει λύση.
Λοιπόν, ποιο γινόμενο p0 δόθηκε στον Γ αν s0=17; Ας ερευνήσουμε τις δυνατές αναλύσεις s0 σε άθροισμα δυο όρων:
Επομένως, η μοναδική δυνατή τιμή του p0 είναι 4·13=52. Με αυτή την τιμή, ο μαθηματικός Γ έχει τη δυνατότητα να μαντέψει τους αριθμούς, διότι απ' όλες τις δυνατές αναλύσεις του 52 σε δυο παράγοντες μόνο μια, η 52=4·13, δίνει περιττό άθροισμα παραγόντων. Συνεπώς, s0=17, p0=52 και οι ζητούμενοι αριθμοί είναι το 4 και το 13.
Η παραπάνω ανάλυση βασίστηκε στο άρθρο των
S. Artyomov, Y. Gimatov και V. Fyodorov,
“Κρυφές πληροφορίες ή, πως δυο μυστικά μας δίνουν μια βεβαιότητα”
περιοδικό QUANTUM, Σεπτέμβριος/Οκτώβριος 1996.
Δυο μαθηματικοί - ο Γ. και ο Α. - συνελήφθησαν από μια φυλή ανθρωποφάγων. Όταν τους παρουσίασαν στον αρχηγό της φυλής με έκπληξη διαπίστωσαν ότι αυτός ήταν απόφοιτος της φυσικομαθηματικής σχολής του πανεπιστημίου Αθηνών και λάτρης των μαθηματικών. Γι αυτό τους έδωσε μια ευκαιρία για να γλιτώσουν, αρκεί να έλυναν το πρόβλημα που θα τους έθετε. Τους είπε:
"Έχω σκεφτεί δυο ακέραιους και θετικούς αριθμούς χ και ψ. Θα αποκαλύψω τώρα στον Γ, κρυφά από τον Α, το γινόμενο (p0=χ·ψ) αυτών των αριθμών.
Και μετά θα πω στον Α, κρυφά από τον Γ, το άθροισμά τους (s0=χ+ψ)."
(Το άθροισμά των αριθμών είναι είναι μικρότερο του 100 και είναι διαφορετικοί από τη μονάδα).
Στη συνέχεια ζήτησε από τους δυο μαθηματικούς να βρουν τους αριθμούς.
Ακολούθησε ο παρακάτω διάλογος μεταξύ των μαθηματικών Γ και Α
Γ: "Απ' ότι φαίνεται δεν μπορώ να βρω τους αριθμούς" (γ1)
Α: "Το ήξερα ότι δεν θα τους βρεις!" (α1)
Γ: "Αφού είναι έτσι τώρα τους βρήκα!" (γ2)
Α: "Τώρα τους βρήκα και εγώ!" (α2)
Μπορούμε από τον παραπάνω διάλογο να βρούμε ποιοι είναι οι αριθμοί;
Με μια πρώτη ματιά αυτό φαίνεται αδύνατον ! Πως μπορούμε να βρούμε τους αριθμούς όταν δεν έχει δοθεί καμία πληροφορία γι αυτούς; Κι όμως μπορούμε !
Υποθέτουμε –χωρίς να βλάπτεται η γενικότητα – ότι χ≤ψ.
Ένας τρόπος να βρούμε τους αριθμούς είναι η μέθοδος της δοκιμής και του λάθους:
να ελέγξουμε όλα τα ζεύγη των αριθμών που ικανοποιούν τις συνθήκες
2≤χ≤ψ≤97 (1)
και4≤s0≤99 (2)
– υπενθυμίζεται ότι s0=χ+ψ – για να δούμε ποια από αυτά «επιβιώνουν» από τον διάλογο (γ1) έως (α2). Αλλά κάτι τέτοιο είναι βαρετό και γι αυτό θα περιορίσουμε την έρευνα.Η εικασία των Goldbach - Euler
Ποιες πληροφορίες μπορούμε να εξαγάγουμε από τις προτάσεις (γ1) και (α1);
Η πρώτη πρόταση μας λέει ότι το p0 (= χ·ψ) δεν παραγοντοποιείται μονοσήμαντα σε γινόμενο δυο αριθμών που ικανοποιούν τις ανισότητες (1) και (2). (πρόταση γ11)
Η δεύτερη πρόταση σημαίνει ότι με όποιον τρόπο κι αν αναλύσουμε το s0 σε άθροισμα δυο αριθμών που ικανοποιούν την ανισότητα (1), το γινόμενο των προσθετέων θα έχει την ιδιότητα γ11. (πρόταση α11)
Η πρώτη συνθήκη εξαιρεί μερικά γινόμενα, η δεύτερη αποκλείει ορισμένα αθροίσματα. Ειδικά από την (α11) έπεται ότι είναι αδύνατον να παρασταθεί το s0 ως άθροισμα δυο πρώτων. (Διαφορερικά το γινόμενο αυτών των πρώτων έχει μια και μοναδική παραγοντοποίηση σε δυο παράγοντες που ικανοποιούν τις ανισότητες (1) και (2) και επομένως δεν ικανοποιεί την (γ11)).
Κάθε άρτιος αριθμός, όμως που ικανοποιεί την ανισότητα (2) γράφεται ως άθροισμα δυο πρώτων (αυτό μπορούμε να το πιστοποιήσουμε άμεσα για όλους τους αριθμούς
4, 6, 8, .......,98
Άρα το s0 είναι περιττό. Επιπλέον το (s0-2) είναι σύνθετος αριθμός – διαφορετικά το s0=2+(s0-2) είναι μια παράσταση του s0 ως άθροισμα δυο πρώτων. Αν απορρίψουμε τους αριθμούς που δεν ικανοποιούν αυτές τις συνθήκες, καταλήγουμε σε 24 δυνατές τιμές του s0. To επιχείρημα....
που χρησιμοποιήσαμε παραπάνω – ότι όλοι οι άρτιοι αριθμοί από το 4 έως το 98 μπορούν να γραφούν ως άθροισμα δυο πρώτων – συνδέεται με ένα συναρπαστικό μαθηματικό πρόβλημα. Το 1972, ένα μέλος της Ακαδημίας των Επιστημών της Αγίας Πετρούπολης, ο Christian Goldbach (Γερμανός που προσέφερε τις υπηρεσίες του στο ρωσικό κράτος) έστειλε μια επιστολή στον Leonard Euler στην οποία διατύπωνε την εικασία ότι κάθε περιττός αριθμός μεγαλύτερος του 5 μπορεί να παρασταθεί ως άθροισμα τριών πρώτων. Ο Euler στην απάντησή του πρότεινε την εικασία ότι κάθε άρτιος αριθμός μεγαλύτερος του 2 γράφεται ως άθροισμα δυο πρώτων. (Δεν είναι δύσκολο να συναγάγουμε την εικασία του Goldbach από την υπόθεση Euler – δοκιμάστε το μόνοι σας!).
Και οι δυο εικασίες για δυο σχεδόν αιώνες, φαινόταν αδύνατον να αποδειχθούν, παρότι είχαν επαληθευτεί με άμεση έρευνα για όλους τους αριθμούς έως το 9.000.000.
Το 1930, ο σπουδαίος ρώσος μαθηματικός L.G. Shnirelman απέδειξε ότι υπάρχει ένας αριθμός k τέτοιος ώστε κάθε ακέραιος n>1 να παρίσταται ως άθροισμα k το πολύ πρώτων αριθμών. Στην απόδειξη του Shnirelman ο αριθμός k ήταν μάλλον μεγάλος. Αργότερα αποδείχθηκε ότι το θεώρημα αληθεύει για k=20.
Το 1934, ένας άλλος διάσημος ρώσος μαθηματικός, ο I. M. Vinogradov, απέδειξε ότι κάθε αριθμός n>n0, για κάποιο συγκεκριμένο n0, γράφεται ως άθροισμα τριών πρώτων. Η σταθερά του Vinogradov είναι πολύ μεγάλος αριθμός
Όσον αφορά την εικασία του Εuler δεν έχει επιτευχθεί κάποια σημαντική πρόοδος προς την κατεύθυνση της απόδειξής της. (διαβαστε περισσότερα ΕΔΩ)
Δεύτερος γύρος
Μπορούμε να μειώσουμε κι άλλο το πλήθος των υποψήφιων για το s0: μπορούμε να συμπεράνουμε από την πρόταση (α11) ότι
s0<55 (3)
Για να δούμε τον λόγο που ισχύει αυτό, ας υποθέσουμε ότι, αντίθετα 55≤s0. Τότε, το s0 δεν ικανοποιεί την (α11): μπορούμε να το αναλύσουμε ως άθροισμα δυο όρων που ικανοποιούν την ανισότητα (1), το γινόμενο των οποίων δεν ικανοποιεί τη συνθήκη (γ11). Η ανάλυση είναι s0=53+(s0-2). Πραγματικά, το γινόμενο 53·( s0-2) παραγοντοποιείται μόνο με ένα τρόπο σε γινόμενο παραγόντων που το άθροισμά τους δεν υπερβαίνει το 100, διότι ο ένας από τους δύο έχει αναγκαστικά τη μορφή 53d – αφού το 53 είναι πρώτος - και είναι μεγαλύτερος από το 100 αν d>1. Άρα d=1, και η παραγοντοποίηση είναι μοναδική. Αυτό όμως έρχεται σε αντίθεση με την ιδιότητα (α11) του s0 !Μετά την απόδειξη της ανισότητας (3), το πλήθος των δυνατών τιμών του s0 μειώνεται σε έντεκα:
11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53 (4)
Ας προσπαθήσουμε να ανακαλύψουμε ποιοι από αυτούς του αριθμούς συμφωνούν με τη συνθήκη (α11) χωρίς άμεση έρευνα. Έστω s ένας από τους αριθμούς (4). Το s είναι περιττό, συνεπώς όταν δυο αριθμοί αθρoιζόμενοι μας δίνουν το s, ο ένας τους είναι άρτιος και ο άλλος περιττός. Επομένως, μπορούμε να γράψουμε s=2a+m. Αν το s δεν ικανοποιεί τη συνθήκη (α11), τότε για κάποιο συγκεκριμένο a υπάρχει μια και μοναδική παραγοντοποίηση του γινομένου 2am.Αυτό το a δεν μπορεί να ισούται με τη μονάδα, διότι υπάρχουν τουλάχιστον δυο παραγοντοποιήσεις του 2m. Πράγματι, ας υποθέσουμε ότι a=1. Τότε, ο αριθμός m είναι σύνθετος, οπότε μπορούμε να γράψουμε m=uv, όπου u>2 και v>2, ενώ και οι δυο παραγοντοποιήσεις
2m=2u·v=2·uv
μας ικανοποιούν:2+uv=2+m=s≤100
και2u+v=2+uv-(u-1)(v-2)<2+uv≤100
Έπεται ότι a≥2. Τώρα, είτε a=m είτα a≠m, μπορούμε να εξετάσουμε τις δυο περιπτώσεις ξεχωριστά. Αν a≠m, τότε η p=2a·m και η p=2m·a είναι δυο διαφορετικές παραγοντοποιήσεις. Αφού 2a+m=s<100 και η παραγοντοποίηση του p είναι μοναδική, πρέπει να έχουμε 2m+a≥100. Ταυτόχρονα, από την s=2a+m<53, έπεται ότι m≤53-2a, και επομένως 2m+a≤106-3a, άρα a≤2. Σ' αυτή την περίπτωση, λοιπόν έχουμε a=2, 2m+a=100 και m=49, οπότε οδηγούμαστε στη μοναδική “ύποπτη” τιμή s=53 και στην ανάλυσή της 53=4+49. Στην περίπτωση a=m, ο αριθμός s=3a διαιρείται με το 3. Δυο μόνο από τους αριθμούς (4) είναι πολλαπλάσια του 3: το 27 και το 51. Οι “ύποπτες” αναλύσεις τους είναι 27=18+9 και 51=34+17. Ο αριθμός 51 δεν ικανοποιεί την (α11) – πράγματι το γινόμενο 17·34 παραγοντοποιείται μόνο με έναν τρόπο σε δυο παράγοντες με άθροισμα μικρότερο του 100, και επομένως μπορούμε να το εξαιρέσουμε από τη λίστα των “υποψηφίων για το s0”. Οι αριθμοί 27 και 53 εξακολουθούν να είναι στη λίστα: ικανοποιούν την (α11), διότι για το 27 έχουμε 9·18=2·81 και 2+81<100, και για το 53 έχουμε 4·49=7·28 και 7+28<100. Επομένως, απομένουν δέκα “υποψήφιοι”:11, 17,23, 27, 29, 35, 37, 41, 47 και 53.
Όλοι τους ικανοποιούν την (α11)."Τώρα τους βρήκα και εγώ!"
Τέλος, ας χρησιμοποιήσουμε τις προτάσεις (γ2) και (α2). Θα μπορούσαμε να τις ερμηνεύσουμε όπως τις δυο προηγούμενες. Υπάρχει όμως ένας συντομότερος τρόπος. Από την (α2) και την ανισότητα (3): s0<55, συμπεραίνουμε ότι s0<33 (5) Ας υποθέσουμε ότι αυτό δεν αληθεύει. Τότε, s0≥33, και ο μαθηματικός Α, αναλύοντας το s0 σε άθροισμα δυο όρων με κάθε δυνατό τρόπο, θα έβρισκε τις εξής παραλλαγές: s0=(s0-31)+31=(s0-29)+29 Η πορεία των σκέψεών του θα ήταν τότε η εξής: αν είχε δοθεί στον Γ το γινόμενο (s0-31)·31, τότε, αν χρησιμοποιούσε την εκτίμηση (3): s0<55 και το γεγονός ότι ο 31 είναι πρώτος αριθμός, θα είχε καταλάβει ότι το (s0-31)·31 έχει μόνο μια παραγοντοποίηση τέτοια ώστε το άθροισμα των δυο πρώτων όρων της να ικανοποιεί την ανισότητα (3). Τότε ο Γ θα μάντευε τους άγνωστους αριθμούς. Το ίδιο επιχείρημα, όμως, εφαρμόζεται και στο γινόμενο (s0-29)·29. Επομένως, στην περίπτωση s0≥33, o μαθηματικός Α δεν θα μπορούσε να προσδιορίσει ακριβώς τους αριθμούς χ και ψ ακόμη και μετά τη δήλωση του (γ2) του Γ, αντίθετα απ' ό,τι συνέβη στην ιστορία μας. Άρα η ανισότητα (5): s0<33 είναι πραγματικά αληθής, και έτσι απομένουν μόνο πέντε αριθμοί:
11, 17, 23, 27, 29.
Επιπλέον, αν:όπου p περιττός πρώτος και n>1, τότε ο Γ μπορεί να προσδιορίσει με βεβαιότητα τους μυστικούς αριθμούς, διότι υπάρχει μόνο ένα περιττό άθροισμα της μορφής
συγκεκριμένα, το
Έτσι, αν το s0 έχει δυο αναπαραστάσεις της μορφής
τότε ο Α δεν μπορεί να βρει την απάντηση και να κάνει τη δήλωση (α2). Αυτή η παρατήρηση εξαιρεί τρεις ακόμη αριθμούς, τους
11=4+7=8+3, 23 και 27,
και αφήνει στη λίστα: το 17 και το 29.Τώρα τους βρήκαμε κι εμείς !
Στην περίπτωση του αριθμού s0=29, το τελευταίο επιχείρημα δεν ισχύει, διότι υπάρχει μόνο μια αναπαράσταση της μορφής
με p περιττό πρώτο (29=16+13). Μπορούμε, όμως, να το χρησιμοποιήσουμε ελαφρά τροποποιημένο για την ανάλυση: 29=4+25. Στην περίπτωση p0=4·25 έχουμε μόνο ένα ακόμη δυνατό περιττό άθροισμα εκτός από το 29, το 25=20+5 (προφανώς 4·25=5·35), αλλά τότε το 25-2 είναι πρώτος, ενώ το s0-2 πρέπει να είναι σύνθετος. Έτσι, σ' αυτή την περίπτωση είναι και πάλι αδύνατον να μαντέψει ο Α τους αριθμούς, συνεπώς η λίστα των υποψηφίων περιορίζεται σε έναν αριθμό, τον 17 – δηλαδή, είτε s0=17 είτε το πρόβλημα δεν έχει λύση.
Λοιπόν, ποιο γινόμενο p0 δόθηκε στον Γ αν s0=17; Ας ερευνήσουμε τις δυνατές αναλύσεις s0 σε άθροισμα δυο όρων:
17=2+15=3+14=...=8+9
Για καθένα από τα αντίστοιχα γινόμενα, εκτός από το 4·13, Γ θα ήταν αδύνατον να μαντέψει την απάντηση και να κάνει τη δήλωση (γ2). Για παράδειγμα, στην περίπτωση της ανάλυσης 17=2+15, έχουμε p0=2·15=30=5·6, αλλά και το 17 και το 11=5+6 ικανοποιούν την ιδιότητα (α11).Επομένως, η μοναδική δυνατή τιμή του p0 είναι 4·13=52. Με αυτή την τιμή, ο μαθηματικός Γ έχει τη δυνατότητα να μαντέψει τους αριθμούς, διότι απ' όλες τις δυνατές αναλύσεις του 52 σε δυο παράγοντες μόνο μια, η 52=4·13, δίνει περιττό άθροισμα παραγόντων. Συνεπώς, s0=17, p0=52 και οι ζητούμενοι αριθμοί είναι το 4 και το 13.
Η παραπάνω ανάλυση βασίστηκε στο άρθρο των
S. Artyomov, Y. Gimatov και V. Fyodorov,
“Κρυφές πληροφορίες ή, πως δυο μυστικά μας δίνουν μια βεβαιότητα”
περιοδικό QUANTUM, Σεπτέμβριος/Οκτώβριος 1996.
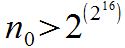
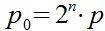


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου